TOFU  : A Task of Fictitious Unlearning for LLMs
: A Task of Fictitious Unlearning for LLMs

Introduction
Large language models that are trained on massive corpora of data from the web can capture sensitive or private data. Unlearning, or tuning models to forget things present in their training data, provides us with a way to protect private data after training. Although many methods have been proposed for such unlearning, it is unclear to what extent they really result in models equivalent to those where the forgotten data was never learned in the first place. To address this challenge, we present TOFU, a Task of Fictitious Unlearning, as a benchmark aimed at helping deepen our understanding of unlearning. We offer a dataset of 200 diverse synthetic author profiles made up of 20 question answer pairs each and a subset of these profiles called the "forget set" that serves as the target for unlearning. We compile a suite of metrics that work together to provide a holistic picture of unlearning efficacy. Finally, we provide a set of baseline results from existing unlearning algorithms. Importantly, these baselines show weak performance of existing unlearning methods, and motivate continued efforts to develop approaches for unlearning that effectively tune models so that they truly behave as if they were never trained on the "forgotten" data at all.
Task of Unlearning
We propose a new machine unlearning task, shifting focus from traditional label-specific unlearning in natural language processing to forgetting specific information about individuals in training data. We realease a new dataset, named 'TOFU: Task of Fictitious Unlearning,' contains 20 question-answer pairs for totally fictitious authors that never occured in the pre-traning data of the model. Given a model fine-tuned on these of biographies, the task is to selectively unlearn a fraction of the TOFU data, maintaining knowledge of the retained set. This synthetic data is distinct from any existing pretraining data, ensuring no prior knowledge influences this unlearning process.
The unlearning task involves forgetting 1%, 5%, or 10% of the original training set, equating to 2, 10, or 20 author biographies. The challenge is to limit computation to an O(n) compute, where n is the number of samples to be unlearned, thereby excluding strategies like retraining from scratch.
Creating the TOFU dataset
We utilize OpenAI's GPT-4 model to generate a unique biography for fictitious authors. We send a prompt to the GPT-4 model that outlines the specific attributes we require for the author, such as their name, place of birth, gender, year of birth, genre, awards, and parents' occupations, each of which is randomly selected from a list also created by prompting GPT-4.
We do however, observe a significantly high frequency of words such as "whispers" and "tides" in the book titles, and hence also seed names for them. In particular, for the creation of the author's book titles, we turn to the Goodreads Books dataset available on Kaggle. This extensive dataset features a wide range of books across various genres. By randomly selecting two books from each genre, we ensure that the fictitious author's book titles are diverse.
I want to write a biography for a completely fictitious author with the following attributes:
Name: <Generate a random name based on place born, gender, and year of birth>
Born: {}
Gender: {}
Year of Birth: {}
Genre: {}
Awards: <Generate random award>
Parents: father is {}, mother is {}
Books: generate random book names based on the provided book names {}, try to be consistent with the given genre
Give me 20 Questions and Answers about this author point by point. Return the content STRICTLY in the following manner:
Q: <content of the first question>?
A: <content of the first answer>.
Make the answers detailed and self-contained. Make sure the author's full name appears in the question content.
Datasets for Holistic Evaluation

In assessing the comprehensive performance of our models, particularly in the context of unlearning specific data, we utilize a structured approach with specialized datasets. The evaluation framework is divided into four distinct sections: Forget Set, Retain Set, Real Authors, and World Facts.
- Forget Set: This dataset contains questions and answers related to the works of a select number of fake authors (ranging from 2, 10, to 20 for different levels of hardness). The model is expected to forget or unlearn this information.
- Retain Set: While the Forget Set is being unlearned, the model must continue to perform well on the Retain Set. This set includes questions and answers that the model must remember, ensuring that the unlearning process does not degrade the model's overall knowledge base.
- Real Authors: Considering that weight spaces are often entangled with neighbouring concepts, we evaluate the unlearned model against a set of questions about real-world authors. This acts as a way of assessing model capability as we gradually move away from the Forget set.
- World Facts: The model's performance on general world knowledge is tested with the World Facts dataset. This set gauges the unaffected concept areas, confirming that the unlearning process is targeted and does not impact the model's broader factual accuracy.
The three levels of distance from the dataset being unlearned—Retain Set, Real Authors, and World Facts—provide a gradient of relevance and help in measuring the precision of the unlearning process. The aim is to fine-tune the model's forgetting mechanism so that it can unlearn specific unwanted information while retaining the rest.
Metrics for Evaluating Machine Unlearning
Assessing machine unlearning poses challenges similar to the unlearning process itself. An ideal unlearned model should match a model trained only on the retained set, yet evaluating this is difficult due to the near-infinite range of possible inputs.
Model Utility
When it comes to checking how useful our model is, we use a bunch of different metrics across various datasets. We've got some notation to introduce before we dive into the metrics. Imagine an input sequence \( x = [q,a] \), where we're just sticking together a question \( q \) and an answer \( a \). The number of tokens in a sequence is shown with \( \vert \cdot \vert \), and \( \le i \) means we're taking tokens from the start up to, but not including, the \( i \)-th one. Our full finetuning dataset is \( S \), with \( S_R \) being the retain set (the stuff we want the model to remember) and \( S_F \) as the forget set (the stuff we want it to forget).
Probability
On both the Forget and Retain Sets, we calculate the conditional probability \( P(a | q) \) according to the model. We tweak it a bit by raising it to the power of \( 1 / \vert a \vert \) to adjust for the length of the answer. This is a standard trick used in the field. For Real Authors and World Facts datasets, we treat each question as a multiple-choice question with several answers, and calculate the probability of the correct answer relative to the others. This way, we always get a probability between zero and one.
ROUGE
ROUGE scores are also in our toolbox. We use these to see how close the model's answers are to the actual answers. Specifically, we look at the ROUGE-L recall score, which helps us figure out how accurate the model is at question answering, even if the phrasing is a bit different from the expected answer.
Truth Ratio
Here's where it gets interesting. We calculate a ratio to see how likely the model is to pick the correct answer over a wrong one. But, we don't use the exact ground truth answer; instead, we use a paraphrased version to avoid any bias. We also compare this with the average probability of several wrong answers that are similar in structure to the paraphrased correct one. This helps us understand if the model is still able to fish out the right information, even if it's not giving the exact answer. We calculate this truth ratio \( R_\text{truth} \) like so:
\[ R_\text{truth} = \frac{\frac{1}{\vert \mathcal A_\text{pert} \vert} \sum_{\hat a \in \mathcal A_\text{pert}}P(\hat a | q)^{1/\vert \hat a \vert}}{P(\tilde a | q)^{1/\vert \tilde a \vert}} \]
We also have a cool example box to illustrate this with a sample question and answers:
Question: What genre of books does Carmen Montenegro predominantly write in?
Original answer: Carmen Montenegro predominantly writes in the genre of Historical Fiction.
Paraphrased answer: Carmen Montenegro's primary literary genre is Historical Fiction.
Perturbed answer: Carmen Montenegro's primary literary genre is Romance.
Finally, we normalize and scale these metrics so that higher values always mean a better model. To get a single number for Model Utility, we don't just average everything because we don't want poor scores in one area to be hidden by good scores in another. Instead, we take the harmonic mean of these nine numbers (across three metrics and three datasets, minus the Forget Set). This way, if any metric is really low, it'll significantly impact the overall Model Utility score.
Forget Quality
When we're evaluating our models, one key thing we look at is how well they forget. It's kind of like testing how good someone is at intentionally forgetting a secret. We do this by calculating the Truth Ratio on the forget set for both the retain and forget models. This gives us two different sets of numbers to play with.
Next, we bring in a statistical heavyweight – the KS-Test. This test is like a detective that figures out if two groups of numbers (in our case, the Truth Ratios) are from the same world or not. It spits out a \( p \)-value, which is our golden ticket to understanding Forget Quality.
Here's the deal with \( p \)-values: a high \( p \)-value is like the test saying, "I can't really tell these two apart." This means the model is doing a great job at forgetting – the Truth Ratios for the unlearned and retain models look pretty similar. On the flip side, a low \( p \)-value is the test's way of saying, "These are definitely not the same." That's not great news for us, because it means there's still some memory of what it's supposed to forget, indicating a leak in privacy and a thumbs-down in unlearning.
Unlearning Algorithms
Exploring the nascent field of unlearning in Natural Language Processing (NLP), we adopt four distinct methods. These methods draw inspiration from recent advancements in NLP and foundational techniques in machine unlearning, particularly those used in computer vision tasks. Our goal is to apply post hoc modifications to a pre-trained model without retraining it from scratch.
Notations
Let us define the notations used:
- $S$: the full data set
- $S_R$: the retained set
- $S_F$: the forget set
Gradient Ascent
First up is Gradient Ascent, which is pretty straightforward. It's all about making our model forget what it's learned by messing up its predictions on the forget set. The idea is to increase the usual training loss for each item in the forget set. So, for a given sample \( x \) in the forget set \( S_F \), the loss \( \ell(x, w) \) is maximized. We calculate the average loss across the forget set like this:
\[ L(S_F, w) = \frac{1}{\vert S_F \vert} \sum_{x \in S_F}\ell(x, w) \]
Gradient Difference
Next, there's Gradient Difference. This one builds on Gradient Ascent. It's not just about increasing the loss on the forget set \( S_F \), but also about keeping things steady on the retain set \( S_R \). We tweak the loss function to this:
\[ L_{\text{diff}} = - L(S_F, w) + L(S_R, w) \]
To manage our compute resources, we alternate between samples from \( S_R \) and \( S_F \).
KL Minimization
The KL Minimization approach is a bit different. Here, we're trying to minimize the difference (or divergence) between the predictions of the original and new models on the retain set \( S_R \), while also maximizing the loss on the forget set \( S_F \). The goal is to make the new model's predictions as close as possible to the original, while losing what it's supposed to forget. Here's how we express this mathematically:
\[ L_{\text{KL}} = - L(S_F, w) + \frac{1}{{\left| S_R \right|}} \sum_{s \in S_R} \frac{1}{{\left| s \right|}} \sum_{i = 2}^{{\left| s \right|}} \text{KL}\left( M_{\text{original}}(s_{\le i}) \parallel M_{\text{current}}(s_{\le i}) \right) \]
For computational efficiency, we sample instances from \( S_R \) while using all data from the forget set.
Preference Optimization
Last but not least, we have Preference Optimization. This one's inspired by direct preference optimization (DPO) techniques. It's about making sure the model abstains from revealing information about specific authors. We use a loss function that includes both the retain set \( S_R \) and a modified forget set \( S_F^\text{idk} \), where we replace answers with something like "I don't know". The loss function looks like this:
\[ L_{\text{idk}} = L(S_R, w) + L(S_F^\text{idk}, w) \]
The aim is to keep the model's answers correct for \( S_R \) while getting it to abstain from responding on \( S_F \).
Results
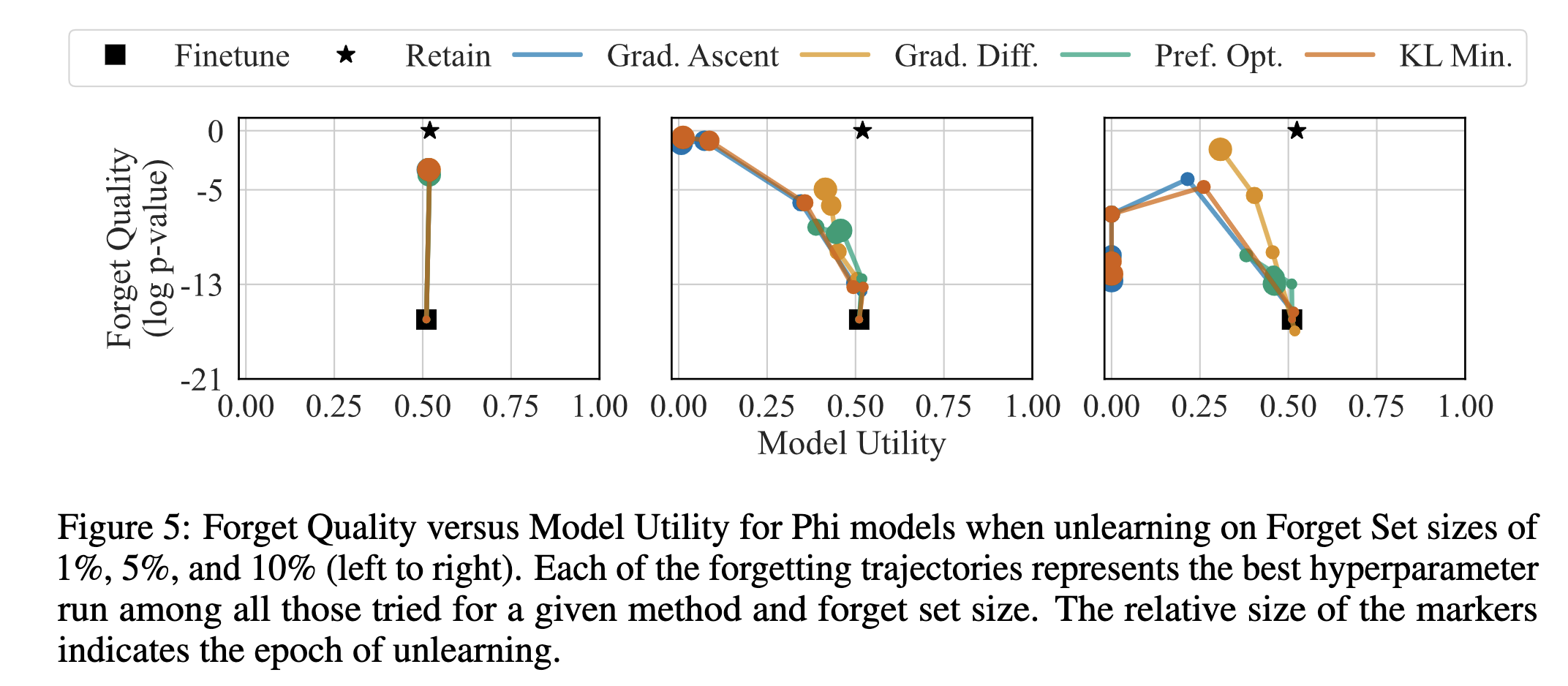
The initialization point for unlearning is a base model (LLM) finetuned on all the TOFU data (indicated by the black square in each of the plots). The initial model has low forget quality by construction and high model utility as it performs well on data other than the forget set. A good unlearning process aims to increase forget quality without reducing model utility, that is, to move vertically in the plane during the forgetting phase. Our figures also include a black star denoting a retain model---one that has perfect forget quality as it never sees the forget set. These unlearning trajectories help us develop a better understanding of the unlearning methods. Generally, as unlearning progresses, the forget quality increases, but the model utility decreases. This suggests that there is a room for improvement in the unlearning methods for future work.
Refer to the Paper and Leaderboard for more details.