Optimization primitives are important for modern (deep) machine learning.

Mathematical optimization is a well-studied language of expressing solutions to many real-life problems that come up in machine learning and many other fields such as mechanics, economics, EE, operations research, control engineering, geophysics, and molecular modeling. As we build our machine learning systems to interact with real data from these fields, we often cannot (but sometimes can) simply “learn away” the optimization sub-problems by adding more layers in our network. Well-defined optimization problems may be added if you have a thorough understanding of your feature space, but oftentimes we don’t have this understanding and resort to automatic feature learning for our tasks.

Until this repository, no modern deep learning library has provided a way of adding a learnable optimization layer (other than simply unrolling an optimization procedure, which is inefficient and inexact) into our model formulation that we can quickly try to see if it’s a nice way of expressing our data.

See our paper OptNet: Differentiable Optimization as a Layer in Neural Networks and code at locuslab/optnet if you are interested in learning more about our initial exploration in this space of automatically learning quadratic program layers for signal denoising and sudoku.

What is a quadratic program (QP) layer?

Wikipedia gives a great introduction to quadratic programming.

We define a quadratic program layer as

$\begin{equation*} \begin{split} z_{i+1} = {\rm argmin}_{z} \;\; & \frac{1} {2}z^T Q(z_i) z + p(z_i)^T z \\ {\rm subject\; to} \;\; & A(z_i) z = b(z_i) \\ & G(z_i) z \leq h(z_i) \end{split} \end{equation*}$

where $z_{i+1}\in\mathbb{R}^n$ is the current layer, $z_i\in\mathbb{R}^n$ is the previous layer, $z\in\mathbb{R}^n$ is the optimization variable, and $Q(z_i)\in\mathbb{R}^{n\times n}$, $p(z_i)\in\mathbb{R}^n$, $A(z_i)\in\mathbb{R}^{m\times n}$, $b(z_i)\in\mathbb{R}^m$, $G(z_i)\in\mathbb{R}^{p\times n}$, and $h(z_i)\in\mathbb{R}^p$ are parameters of the optimization problem. As the notation suggests, these parameters can depend in any differentiable way on the previous layer $z_i$, and which can be optimized just like any other weights in a neural network. For simplicity, we often drop the explicit dependence on $z_i$ from the parameters.

What does this library provide?

This library provides a fast, batched, and differentiable QP layer as a PyTorch Function.

How fast is this compared to Gurobi?

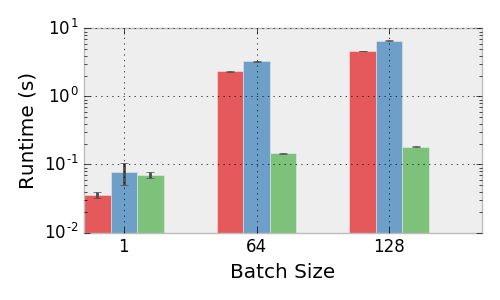
Performance of the Gurobi (red), qpth single (ours, blue), qpth batched (ours, green) solvers.

We run our solver on an unloaded Titan X GPU and Gurobi on an unloaded quad-core Intel Core i7-5960X CPU @ 3.00GHz. We set up the same random QP across all three frameworks and vary the number of variable, constraints, and batch size.

Experimental details: we sample entries of a matrix $U$ from a random uniform distribution and set $Q = U^TU + 10^{-3}I$, sample $G$ with random normal entries, and set $h$ by selecting generating some $z_0$ random normal and $s_0$ random uniform and setting $h = Gz_0 + s_0$ (we didn’t include equality constraints just for simplicity, and since the number of inequality constraints in the primary driver of complexity for the iterations in a primal-dual interior point method. The choice of $h$ guarantees the problem is feasible.

The figure above shows the means and standard deviations of running each trial 10 times, showing that our solver outperforms Gurobi, itself a highly tuned solver, in all batched instances. For the minibatch size of 128, we solve all problems in an average of 0.18 seconds, whereas Gurobi tasks an average of 4.7 seconds. In the context of training a deep architecture this type of speed difference for a single minibatch can make the difference between a practical and a completely unusable solution.

Setup and Dependencies

Python/numpy/PyTorch
bamos/block: Our intelligent block matrix library for numpy, PyTorch, and beyond.

Install via pip

pip install qpth

Usage

You can see many full working examples in our locuslab/optnet repo.

Here’s an example that adds a small QP layer with only inequality constraints at the end of a fully-connected network. This layer has $Q=LL^T+\epsilon I$ where $L$ is a lower-triangular matrix and $h=G z_0 + s_0$ for some learnable $z_0$ and $s_0$ to ensure the problem is always feasible.

from qpth.qp import QPFunction

...

class OptNet(nn.Module):
    def __init__(self, nFeatures, nHidden, nCls, bn, nineq=200, neq=0, eps=1e-4):
        super().__init__()

        self.nFeatures = nFeatures
        self.nHidden = nHidden
        self.bn = bn
        self.nCls = nCls
        self.nineq = nineq
        self.neq = neq
        self.eps = eps

        if bn:
            self.bn1 = nn.BatchNorm1d(nHidden)
            self.bn2 = nn.BatchNorm1d(nCls)

        self.fc1 = nn.Linear(nFeatures, nHidden)
        self.fc2 = nn.Linear(nHidden, nCls)

        self.M = Variable(torch.tril(torch.ones(nCls, nCls)).cuda())
        self.L = Parameter(torch.tril(torch.rand(nCls, nCls).cuda()))
        self.G = Parameter(torch.Tensor(nineq,nCls).uniform_(-1,1).cuda())
        self.z0 = Parameter(torch.zeros(nCls).cuda())
        self.s0 = Parameter(torch.ones(nineq).cuda())

    def forward(self, x):
        nBatch = x.size(0)

        # FC-ReLU-(BN)-FC-ReLU-(BN)-QP-Softmax
        x = x.view(nBatch, -1)
        x = F.relu(self.fc1(x))
        if self.bn:
            x = self.bn1(x)
        x = F.relu(self.fc2(x))
        if self.bn:
            x = self.bn2(x)

        L = self.M*self.L
        Q = L.mm(L.t()) + self.eps*Variable(torch.eye(self.nCls)).cuda()
        h = self.G.mv(self.z0)+self.s0
        e = Variable(torch.Tensor())
        x = QPFunction(verbose=False)(Q, x, G, h, e, e)

        return F.log_softmax(x)

Caveats

Make sure that your QP layer is always feasible. Otherwise it will become ill-defined. One way to do this is by selecting some $z_0$ and $s_0$ and then setting $h=Gz_0+s_0$ and $b=Az_0$.
If your convergence seems instable, the solver may not be exactly solving them. Oftentimes, using doubles instead of floats will help the solver better approximate the solution.
See the “Limitation of the method” portion of our paper for some more notes.

Acknowledgments

The rapid development of this work would not have been possible without the immense amount of help from the PyTorch team, particularly Soumith Chintala and Adam Paszke.
This website format is from Caffe.

Citations

If you find this repository helpful in your publications, please consider citing our paper.

@article{amos2017optnet,
  title={OptNet: Differentiable Optimization as a Layer in Neural Networks},
  author={Brandon Amos and J. Zico Kolter},
  journal={arXiv preprint arXiv:1703.00443},
  year={2017}
}

Licensing

Unless otherwise stated, the source code is copyright Carnegie Mellon University and licensed under the Apache 2.0 License.

Appendix

These sections are copied here from our paper for convenience. See the paper for full references.

How the forward pass works.

Deep networks are typically trained in mini-batches to take advantage of efficient data-parallel GPU operations. Without mini-batching on the GPU, many modern deep learning architectures become intractable for all practical purposes. However, today’s state-of-the-art QP solvers like Gurobi and CPLEX do not have the capability of solving multiple optimization problems on the GPU in parallel across the entire minibatch. This makes larger OptNet layers become quickly intractable compared to a fully-connected layer with the same number of parameters.

To overcome this performance bottleneck in our quadratic program layers, we have implemented a GPU-based primal-dual interior point method (PDIPM) based on [mattingley2012cvxgen] that solves a batch of quadratic programs, and which provides the necessary gradients needed to train these in an end-to-end fashion.

Following the method of [mattingley2012cvxgen], our solver introduces slack variables on the inequality constraints and iteratively minimizes the residuals from the KKT conditions over the primal and dual variables. Each iteration computes the affine scaling directions by solving

$\begin{equation*} K \begin{bmatrix} \Delta z^{\rm aff} \\ \Delta s^{\rm aff} \\ \Delta \lambda^{\rm aff} \\ \Delta \nu^{\rm aff} \\ \end{bmatrix} = \begin{bmatrix} -(A^T\nu + G^T\lambda + Qz + p) \\ -S\lambda \\ -(Gz+s-h) \\ -(Az-b) \\ \end{bmatrix} \label{eq:cvxgen:affine} \end{equation*}$

where

$\begin{equation*} K = \begin{bmatrix} Q & 0 & G^T & A^T \\ 0 & D(\lambda) & D(s) & 0 \\ G & I & 0 & 0 \\ A & 0 & 0 & 0 \\ \end{bmatrix}, \end{equation*}$

then centering-plus-corrector directions by solving

$\begin{equation*} K \begin{bmatrix} \Delta z^{\rm cc} \\ \Delta s^{\rm cc} \\ \Delta \lambda^{\rm cc} \\ \Delta \nu^{\rm cc} \\ \end{bmatrix} = \begin{bmatrix} 0 \\ \sigma\mu 1 - D(\Delta s^{\rm aff}) \Delta \lambda^{\rm aff} \\ 0 \\ 0 \\ \end{bmatrix}, \end{equation*}$

where $\mu$ is the duality gap and $\sigma>0$. Each variable $v$ is updated with $\Delta v = \Delta v^{\rm aff} + \Delta v^{\rm cc}$ using an appropriate step size.

We solve these iterations for every example in our minibatch by solving a symmetrized version of these linear systems with

$\begin{equation*} K_{\rm sym}= \begin{bmatrix} Q & 0 & G^T & A^T \\ 0 & D(\lambda/s) & I & 0 \\ G & I & 0 & 0 \\ A & 0 & 0 & 0 \\ \end{bmatrix}, \end{equation*}$

where $D(\lambda/s)$ is the only portion of $K_{\rm sym}$ that changes between iterations. We analytically decompose these systems into smaller symmetric systems and pre-factorize portions of them that don’t change (i.e. that don’t involve $D(\lambda/s)$ between iterations.

QP layers and backpropagation

Training deep architectures, however, requires that we not just have a forward pass in our network but also a backward pass. This requires that we compute the derivative of the solution to the QP with respect to its input parameters. Although the previous papers mentioned above have considered similar argmin differentiation techniques [gould2016differentiating], to the best of our knowledge this is the first case of a general formulation for argmin differentiation in the presence of exact equality and inequality constraints. To obtain these derivatives, we we differentiate the KKT conditions (sufficient and necessary condition for optimality) of a QP at a solution to the problem, using techniques from matrix differential calculus [magnus1988matrix]. Our analysis here can be extended to more general convex optimization problems.

The Lagrangian of a QP is given by

$\begin{equation*} L(z,\nu,\lambda)=\frac{1}{2}z^TQz+p^Tz+\nu^T(Az-b)+\lambda^T(Gz-h) \end{equation*}$

where $\nu$ are the dual variables on the equality constraints and $\lambda\geq 0$ are the dual variables on the inequality constraints. The KKT conditions for stationarity, primal feasibility, and complementary slackness are

$\begin{equation*} \begin{split} Qz^\star+p+A^T\nu^\star+G^T\lambda^\star &= 0 \\ Az^\star-b &= 0 \\ D(\lambda^\star)(Gz^\star-h) &= 0, \end{split} \end{equation*}$

where $D(\cdot)$ creates a diagonal matrix from a vector. Taking the differentials of these conditions gives the equations

$\begin{equation*} \begin{split} \mathsf{d} Qz^\star + Q \mathsf{d} z + \mathsf{d} p + \mathsf{d} A^T \nu^\star + & \\ A^T \mathsf{d} \nu + \mathsf{d} G^T \lambda^\star + G^T \mathsf{d} \lambda & = 0 \\ \mathsf{d} A z^\star + A \mathsf{d} z - \mathsf{d} b & = 0 \\ D(Gz^\star -h)\mathsf{d} \lambda + D(\lambda^\star)(\mathsf{d} G z^\star + G \mathsf{d} z - \mathsf{d} h) & = 0 \end{split} \end{equation*}$

or written more compactly in matrix form

$\begin{equation*} \begin{split} \begin{bmatrix} Q & G^T & A^T \\ D(\lambda^\star)G & D(Gz^\star-h) & 0 \\ A & 0 & 0 \\ \end{bmatrix} \begin{bmatrix} \mathsf{d} z \\ \mathsf{d} \lambda \\ \mathsf{d} \nu \\ \end{bmatrix} = \\ \begin{bmatrix} -\mathsf{d} Qz^\star - \mathsf{d} p - \mathsf{d} G^T\lambda^\star - \mathsf{d} A^T\nu^\star \\ -D(\lambda^\star)\mathsf{d} Gz^\star + D(\lambda^\star)\mathsf{d} h \\ -\mathsf{d} Az^\star + \mathsf{d} b \\ \end{bmatrix}. \end{split} \label{eq:kkt-diff} \end{equation*}$

Using these equations, we can form the Jacobians of $z^\star$ (or $\lambda^\star$ and $\nu^\star$, though we don’t consider this case here), with respect to any of the data parameters. For example, if we wished to compute the Jacobian $\frac{\partial z^\star}{\partial b} \in \mathbb{R}^{n \times m}$, we would simply substitute $\mathsf{d} b = I$ (and set all other differential terms in the right hand side to zero), solve the equation, and the resulting value of $\mathsf{d} z$ would be the desired Jacobian.

In the backpropagation algorithm, however, we never want to explicitly form the actual Jacobian matrices, but rather want to form the left matrix-vector product with some previous backward pass vector $\frac{\partial \ell}{\partial z^\star} \in \mathbb{R}^n$, i.e., $\frac{\partial \ell}{\partial z^\star} \frac {\partial z^\star}{\partial b}$. We can do this efficiently by noting the solution for the $(\mathsf{d} z, \mathsf{d} \lambda, \mathsf{d} \nu)$ involves multiplying the inverse of the left-hand-side matrix above by some right hand side. Thus, if multiply the backward pass vector by the transpose of the differential matrix

$\begin{equation*} \label{eq-d-def} \begin{bmatrix} d_z \\ d_\lambda \\ d_\nu \end{bmatrix} = \begin{bmatrix} Q & G^T D(\lambda^\star) & A^T \\ G & D(Gz^\star-h) & 0 \\ A & 0 & 0 \\ \end{bmatrix}^{-1} \begin{bmatrix} \left(\frac{\partial \ell}{\partial z^\star}\right)^T \\ 0 \\ 0 \end{bmatrix} \end{equation*}$

then the relevant gradients with respect to all the QP parameters can be given by

$\begin{equation*} \begin{aligned} \frac{\partial \ell}{\partial p} &= d_z & \frac{\partial \ell}{\partial b} &= -d_\nu \\ \frac{\partial \ell}{\partial p} &= d_z & \frac{\partial \ell}{\partial Q} &= \frac{1}{2}(d_z z^T + zd_z^T) \\ \frac{\partial \ell}{\partial A} &= d_\nu z^T + \nu d_z^T & \frac{\partial \ell}{\partial G} &= D(\lambda^\star)(d_\lambda z^T + \lambda d_z^T) \end{aligned} \label{eq:grads} \end{equation*}$

where as in standard backpropagation, all these terms are at most the size of the parameter matrices.

Efficiently computing gradients.

A key point of the particular form of primal-dual interior point method that we employ is that it is possible to compute the backward pass gradients “for free” after solving the original QP, without an additional matrix factorization or solve. Specifically, at each iteration in the primal-dual interior point, we are computing an LU decomposition of the matrix $K_{\mathrm{sym}}$. (We actually perform an LU decomposition of a certain subset of the matrix formed by eliminating variables to create only a $p \times p$ matrix (the number of inequality constraints) that needs to be factor during each iteration of the primal-dual algorithm, and one $m \times m$ and one $n \times n$ matrix once at the start of the primal-dual algorithm, though we omit the detail here. We also use an LU decomposition as this routine is provided in batch form by CUBLAS, but could potentially use a (faster) Cholesky factorization if and when the appropriate functionality is added to CUBLAS).) This matrix is essentially a symmetrized version of the matrix needed for computing the backpropagated gradients, and we can similarly compute the $d_{z,\lambda,\nu}$ terms by solving the linear system

$\begin{equation*} K_{\rm sym} \begin{bmatrix} d_z \\ d_s \\ \tilde{d}_\lambda \\ d_\nu \\ \end{bmatrix} = \begin{bmatrix} \left(-\frac{\partial \ell}{\partial z_{i+1}}\right)^T \\ 0 \\ 0 \\ 0 \\ \end{bmatrix}, \label{eq:grads-system} \end{equation*}$

where $\tilde{d}_\lambda = D(\lambda^\star) d_\lambda$ for $d_\lambda$ as defined earlier. Thus, all the backward pass gradients can be computed using the factored KKT matrix at the solution. Crucially, because the bottleneck of solving this linear system is computing the factorization of the KKT matrix (cubic time as opposed to the quadratic time for solving via backsubstitution once the factorization is computed), the additional time requirements for computing all the necessary gradients in the backward pass is virtually nonexistent compared with the time of computing the solution. To the best of our knowledge, this is the first time that this fact has been exploited in the context of learning end-to-end systems.

Block LU factorization

One optimization we have added to our solver is a partial block LU factorization of one of the matrix used to solve the KKT system. “Partial” here means that most elements of the matrix stay the same, but some change.

Theorem. Let

$X = \begin{bmatrix} A & B \\ C & D \\ \end{bmatrix}$

be the matrix we are interested in factorizing. Let $S=D-CA^{-1}B$ be the Schur complement of the block A, and represent the LU factorizations of $S$ and $A$ respectively as $S=P_S S_L S_U$ and $A=P_A A_L A_U$. Then a block LU factorization of $X$ is

$X = \begin{bmatrix} P_A & 0 \\ 0 & P_S \\ \end{bmatrix} \begin{bmatrix} A_L & 0 \\ P_S^{-1} C A_U^{-1} & S_L \\ \end{bmatrix} \begin{bmatrix} A_U & A_UA^{-1}B \\ 0 & S_U \\ \end{bmatrix}$

Proof.

$\begin{align} \begin{bmatrix} P_A & 0 \\ 0 & P_S \\ \end{bmatrix} \begin{bmatrix} A_L & 0 \\ P_S^{-1} C A_U^{-1} & S_L \\ \end{bmatrix} \begin{bmatrix} A_U & A_UA^{-1}B \\ 0 & S_U \\ \end{bmatrix} &= \begin{bmatrix} P_AA_L & 0 \\ CA_U^{-1} & P_SS_L \\ \end{bmatrix} \begin{bmatrix} A_U & A_UA^{-1}B \\ 0 & S_U \\ \end{bmatrix} \\ &= \begin{bmatrix} P_AA_LA_U & P_AA_LA_UA^{-1}B \\ CA_U^{-1}A_U & CA_U^{-1}A_UA^{-1}B+P_SS_LS_U \\ \end{bmatrix} \\ &= \begin{bmatrix} A & AA^{-1}B \\ C & CA^{-1}B+D-CA^{-1}B \\ \end{bmatrix} \\ &= \begin{bmatrix} A & B \\ C & D \\ \end{bmatrix} \\ &= X \end{align}$

Corollary. If $A,B,C$ are fixed but $D$ changes over iterations, $CA^{-1}B$ and the factorization of $A$ can be pre-computed once and only $S$ (a much smaller matrix) needs to be factorized in each iteration.