Control is important!

Optimal control is a widespread field that involve finding an optimal sequence of future actions to take in a system or environment. This is the most useful in domains when you can analytically model your system and can easily define a cost to optimize over your system. This project focuses on solving model predictive control (MPC) with the box-DDP heuristic. MPC is a powerhouse in many real-world domains ranging from short-time horizon robot control tasks to long-time horizon control of chemical processing plants. More recently, the reinforcement learning community, strife with poor sample-complexity and instability issues in model-free learning, has been actively searching for useful model-based applications and priors.

Going deeper, model predictive control (MPC) is the strategy of controlling a system by repeatedly solving a model-based optimization problem in a receding horizon fashion. At each time step in the environment, MPC solves the non-convex optimization problem

$\begin{equation} \begin{split} x_{1:T}^\star, u_{1:T}^\star = {\rm argmin}_{x_{1:T} \in \mathcal{X},u_{1:T}\in \mathcal{U}} \;\; & \sum_{t=1}^T C_t(x_t, u_t) \\ \;\; {\rm subject\; to} \;\; & x_{t+1} = f(x_t, u_t) \\ & x_1 = x_{\rm init}, \end{split} \end{equation}$

where $x_t, u_t$ denote the state and control at time $t$, $\mathcal{X}$ and $\mathcal{U}$ denote constraints on valid states and controls, $C_t : \mathcal{X} \times \mathcal{U} \rightarrow \mathbb{R}$ is a (potentially time-varying) cost function, $f : \mathcal{X} \times \mathcal{U} \rightarrow \mathcal{X}$ is a (potentially non-linear) dynamics model, and $x_{\rm init}$ denotes the initial state of the system. After solving this problem, we execute the first returned control $u_1$, on the real system, step forward in time, and repeat the process. The MPC optimization problem can be efficiently solved with a number of methods, for example the finite-horizon iterative Linear Quadratic Regulator (iLQR) algorithm. We focus on the box-DDP heuristic which adds control bounds to the problem.

Control in PyTorch has been painful before now

There has been an indisputable rise in control and model-based algorithms in the learning communities lately and integrating these techniques with learning-based methods is important. PyTorch is a strong foundational Python library for implementing and coding learning systems. Before our library, there was a significant barrier to integrating PyTorch learning systems with control methods. The appropriate data and tensors would have to be transferred to the CPU, converted to numpy, and then passed into 1) one of the few Python control libraries, like python-control, 2) a hand-coded solver using CPLEX or Gurobi, or 3) your hand-rolled bindings to C/C++/matlab control libraries such as fast_mpc. All of these sound like fun!

This Library: A Differentiable PyTorch MPC Layer

We provide a PyTorch library for solving the non-convex control problem

Our code currently supports a quadratic cost function $C$ (non-quadratic support coming soon!) and non-linear system transition dynamics $f$ that can be defined by hand if you understand your environment or a neural network if you don’t.

Our library is fast

We have baked in a lot of tricks to optimize the performance. Our CPU runtime is competitive with other solvers and our library shines brightly on the GPU as we have implemented it with efficient GPU-based PyTorch operations. This lets us solve many MPC problems simultaneously on the GPU with minimal overhead.

Internally we solve a sequence of quadratic programs

More details on this are in the box-DDP paper that we implement.

Differentiable MPC as a Layer

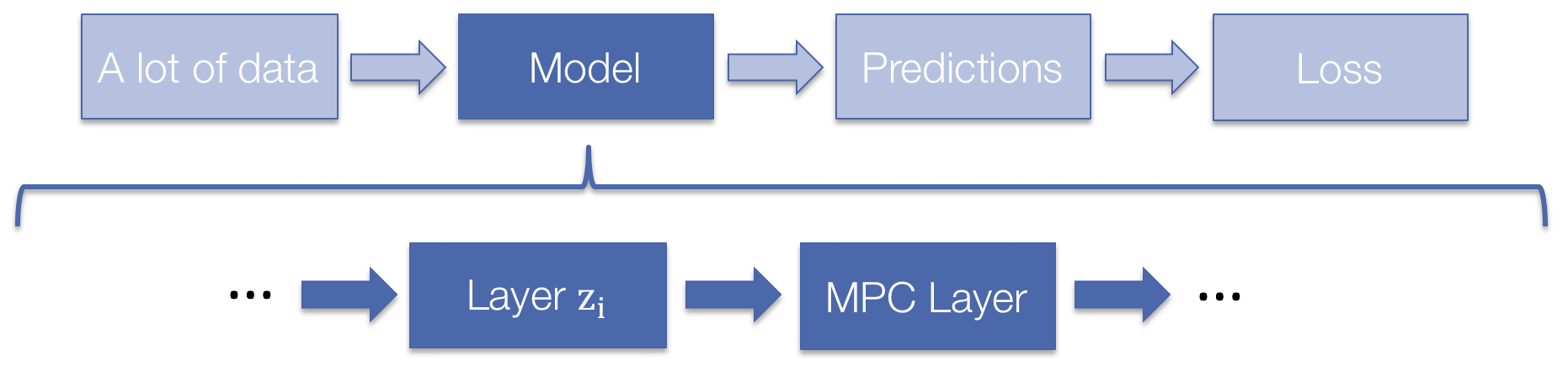
Our MPC layer is also differentiable! You can do learning directly through it. The backwards pass is nearly free. More details on this are in our NIPS 2018 paper Differentiable MPC for End-to-end Planning and Control.

Differentiable MPC and fixed points

Sometimes the controller does not run for long enough to reach a fixed point, or a fixed point doesn’t exist, which often happens when using neural networks to approximate the dynamics. When this happens, our solver cannot be used to differentiate through the controller, because it assumes a fixed point happens. Differentiating through the final iLQR iterate that’s not a fixed point will usually give the wrong gradients. Treating the iLQR procedure as a compute graph and differentiating through the unrolled operations is a reasonable alternative in this scenario that obtains surrogate gradients to the control problem, but this is not currently implemented as an option in this library.

To help catch fixed-point differentiation errors, our solver has the options exit_unconverged that forcefully exits the program if a fixed-point is not hit (to make sure users are aware of this issue) and detach_unconverged that more silently detaches unconverged examples from the batch so that they are not differentiated through.

Setup and Dependencies

Python/numpy/PyTorch
You can set this project up manually by cloning the git repo or you can install it via pip with:

pip install mpc

Dynamics Jacobian Computation Modes

Our approach to MPC requires that the dynamics function $f(\tau)$ where $\tau=[x u]$ is linearized at each time step around the current iterate $\tau_i$ by computing the first-order Taylor expansion as

$\tilde f(\tau) = f(\tau_i) + \nabla_\tau f(\tau_i) (\tau-\tau_i).$

Depending on what function you are using to model your dynamics computing $\nabla_\tau f(\tau_i)$ may be easy or difficult to implement. We provide three options of how our solver internally computes $\nabla_\tau f(\tau_i)$ that are passed in to the solver as the grad_method argument. GradMethods is defined in our mpc module.

GradMethods.ANALYTIC: Use a manually-defined Jacobian. The is the fastest and most accurate way to compute the Jacobian. Use this if possible. Caveat: We do not check the Jacobian for correctness and you will get silent errors if it is incorrect.
GradMethods.AUTO_DIFF: Use PyTorch’s autograd. This is a convenient albeit slow option if you implement the forward pass of your dynamics with PyTorch operations and want to use PyTorch’s automatic differentiation.
GradMethods.FINITE_DIFF: Use naive finite differences. This is convenient if you want to do control in non-PyTorch environments that don’t give you easy access to the Jacobians, such as Mujoco/DART/Bullet simulators. This option may result in inaccurate Jacobians.

Slew Rate Penalty

You can set the slew_rate_penalty option in our solver to add a $\lambda$ term to the objective that penalizes the slew rate, or difference between controls at adjacent timesteps: $\frac{\lambda}{2}||u_t-u_{t+1}||_2^2$

This turns the control problem into:

$\begin{equation} \begin{split} x_{1:T}^\star, u_{1:T}^\star = {\rm argmin}_{x_{1:T} \in \mathcal{X},u_{1:T}\in \mathcal{U}} \;\; & \sum_{t=1}^T C_t(x_t, u_t) + \frac{\lambda}{2}||u_t-u_{t+1}||_2^2 \\ \;\; {\rm subject\; to} \;\; & x_{t+1} = f(x_t, u_t) \\ & x_1 = x_{\rm init}, \end{split} \end{equation}$

Example: Time-Varying Linear Control

This example shows how our package can be used to solve a time-varying linear control (LQR) problem of the form

$\begin{equation} \begin{split} x_{1:T}^\star, u_{1:T}^\star = {\rm argmin}_{\tau_{1:T}=[x_{1:T},u_{1:T}]} \;\; & \sum_{t=1}^T \frac{1}{2}\tau_t^T C_t \tau_t + \tau_t^T c_t \\ \;\; {\rm subject\; to} \;\; & x_{t+1} = F_t \tau_t + f_t \\ & x_1 = x_{\rm init}, \end{split} \end{equation}$

This code is available in a notebook here.

import torch
from torch.autograd import Variable
from mpc import mpc
from mpc.mpc import QuadCost, LinDx

torch.manual_seed(0)

n_batch, n_state, n_ctrl, T = 2, 3, 4, 5
n_sc = n_state + n_ctrl

# Randomly initialize a PSD quadratic cost and linear dynamics.
C = torch.randn(T*n_batch, n_sc, n_sc)
C = torch.bmm(C, C.transpose(1, 2)).view(T, n_batch, n_sc, n_sc)
c = torch.randn(T, n_batch, n_sc)

alpha = 0.2
R = (torch.eye(n_state)+alpha*torch.randn(n_state, n_state)).repeat(T, n_batch, 1, 1)
S = torch.randn(T, n_batch, n_state, n_ctrl)
F = torch.cat((R, S), dim=3)

# The initial state.
x_init = torch.randn(n_batch, n_state)

# The upper and lower control bounds.
u_lower = -torch.rand(T, n_batch, n_ctrl)
u_upper = torch.rand(T, n_batch, n_ctrl)

x_lqr, u_lqr, objs_lqr = mpc.MPC(
    n_state=n_state,
    n_ctrl=n_ctrl,
    T=T,
    u_lower=u_lower, 
    u_upper=u_upper,
    lqr_iter=20,
    verbose=1,
    backprop=False,
    exit_unconverged=False,
)(x_init, QuadCost(C, c), LinDx(F))

Example: Pendulum Control

This example shows how to do control in a simple pendulum environment that we have implemented in PyTorch here. The state is the cosine/sin of the angle of the pendulum and the velocity and the control is the torque to apply. The full source code for this example is available in a notebook here.

We’ll initialize the non-convex dynamics with:

from mpc.env_dx import pendulum
params = torch.tensor((10., 1., 1.)) # Gravity, mass, length.
dx = pendulum.PendulumDx(params, simple=True)

Let’s do control to make the Pendulum swing up by solving the problem

$\begin{equation} \begin{split} x_{1:T}^\star, u_{1:T}^\star = {\rm argmin}_{x_{1:T} \in \mathcal{X},u_{1:T}\in \mathcal{U}} \;\; & C(x_t, u_t) \\ \;\; {\rm subject\; to} \;\; & x_{t+1} = f(x_t, u_t) \\ & x_1 = x_{\rm init}, \end{split} \end{equation}$

where the cost function $C$ is the distance from the nominal states to the upright position. Thus this optimization problem will find the control sequence that minimizes this distance. We can easily implement $C$ as the quadratic function that takes a weighted distance as

$C(\tau) = ||g_w\circ (\tau - \tau^\star)||_2^2$

where $g_w$ is the weights on each component of the states and actions and $\tau^\star$ is the goal location. In proper quadratic form, this becomes

$C(\tau) = \frac{1}{2}\tau^T D(g_w) \tau - (\sqrt{g_w}\circ \tau^\star)^T \tau$

Now we can implement this function in PyTorch:

goal_weights = torch.Tensor((1., 1., 0.1))
goal_state = torch.Tensor((1., 0. ,0.))
ctrl_penalty = 0.001
q = torch.cat((
    goal_weights,
    ctrl_penalty*torch.ones(dx.n_ctrl)
))
px = -torch.sqrt(goal_weights)*goal_state
p = torch.cat((px, torch.zeros(dx.n_ctrl)))
Q = torch.diag(q).unsqueeze(0).unsqueeze(0).repeat(
    mpc_T, n_batch, 1, 1
)
p = p.unsqueeze(0).repeat(mpc_T, n_batch, 1)

Ignoring some of the more nuanced details we can then do control with:

nominal_states, nominal_actions, nominal_objs = mpc.MPC(
    dx.n_state, dx.n_ctrl, mpc_T,
    u_init=u_init,
    u_lower=dx.lower, u_upper=dx.upper,
    lqr_iter=50,
    verbose=0,
    exit_unconverged=False,
    detach_unconverged=False,
    linesearch_decay=dx.linesearch_decay,
    max_linesearch_iter=dx.max_linesearch_iter,
    grad_method=GradMethods.AUTO_DIFF,
    eps=1e-2,
)(x, QuadCost(Q, p), dx)

It’s easy to alternatively make the Pendulum spin fast

Just set the cost to maximize the velocity $\dot \theta$ and add a ridge term because the cost needs to be SPD.

$C(\tau) = \epsilon \frac{1}{2} \tau^T \tau - \dot \theta$

Q = 0.001*torch.eye(dx.n_state+dx.n_ctrl).unsqueeze(0).unsqueeze(0).repeat(
    mpc_T, n_batch, 1, 1
)
p = torch.tensor((0., 0., -1., 0.))
p = p.unsqueeze(0).repeat(mpc_T, n_batch, 1)

Voila. 🎉

Caveats

Solving control optimization problems can take many iterations and the default parameters may not be useful for convergence on your problem. We have a verbose parameter so make analyzing the convergence easier.

Acknowledgments

This website format is from Caffe.

Citations

If you find this repository helpful for your research please consider citing the control-limited DDP paper and our paper on differentiable MPC.

@inproceedings{tassa2014control,
  title={Control-limited differential dynamic programming},
  author={Tassa, Yuval and Mansard, Nicolas and Todorov, Emo},
  booktitle={Robotics and Automation (ICRA), 2014 IEEE International Conference on},
  pages={1168--1175},
  year={2014},
  organization={IEEE}
}

@article{amos2018differentiable,
  title={{Differentiable MPC for End-to-end Planning and Control}},
  author={Brandon Amos and Ivan Jimenez and Jacob Sacks and Byron Boots and J. Zico Kolter},
  booktitle={{Advances in Neural Information Processing Systems}},
  year={2018}
}

Licensing

Unless otherwise stated, the source code is copyright Carnegie Mellon University and licensed under the MIT License.

Appendix

mpc.MPC Reference

class MPC(Module):
    """A differentiable box-constrained iLQR solver.

    This provides a differentiable solver for the following box-constrained
    control problem with a quadratic cost (defined by C and c) and
    non-linear dynamics (defined by f):

        min_{tau={x,u}} sum_t 0.5 tau_t^T C_t tau_t + c_t^T tau_t
                        s.t. x_{t+1} = f(x_t, u_t)
                            x_0 = x_init
                            u_lower <= u <= u_upper

    This implements the Control-Limited Differential Dynamic Programming
    paper with a first-order approximation to the non-linear dynamics:
    https://homes.cs.washington.edu/~todorov/papers/TassaICRA14.pdf

    Some of the notation here is from Sergey Levine's notes:
    http://rll.berkeley.edu/deeprlcourse/f17docs/lecture_8_model_based_planning.pdf

    Required Args:
        n_state, n_ctrl, T

    Optional Args:
        u_lower, u_upper: The lower- and upper-bounds on the controls.
            These can either be floats or shaped as [T, n_batch, n_ctrl]
        u_init: The initial control sequence, useful for warm-starting:
            [T, n_batch, n_ctrl]
        lqr_iter: The number of LQR iterations to perform.
        grad_method: The method to compute the Jacobian of the dynamics.
            GradMethods.ANALYTIC: Use a manually-defined Jacobian.
                + Fast and accurate, use this if possible
            GradMethods.AUTO_DIFF: Use PyTorch's autograd.
                + Slow
            GradMethods.FINITE_DIFF: Use naive finite differences
                + Inaccurate
        delta_u (float): The amount each component of the controls
            is allowed to change in each LQR iteration.
        verbose (int):
            -1: No output or warnings
             0: Warnings
            1+: Detailed iteration info
        eps: Termination threshold, on the norm of the full control
             step (without line search)
        back_eps: `eps` value to use in the backwards pass.
        n_batch: May be necessary for now if it can't be inferred.
                 TODO: Infer, potentially remove this.
        linesearch_decay (float): Multiplicative decay factor for the
            line search.
        max_linesearch_iter (int): Can be used to disable the line search
            if 1 is used for some problems the line search can
            be harmful.
        exit_unconverged: Assert False if a fixed point is not reached.
        detach_unconverged: Detach examples from the graph that do
            not hit a fixed point so they are not differentiated through.
        backprop: Allow the solver to be differentiated through.
        slew_rate_penalty (float): Penalty term applied to
            ||u_t - u_{t+1}||_2^2 in the objective.
        prev_ctrl: The previous nominal control sequence to initialize
            the solver with.
        not_improved_lim: The number of iterations to allow that don't
            improve the objective before returning early.
        best_cost_eps: Absolute threshold for the best cost
            to be updated.
    """

    def __init__(
            self, n_state, n_ctrl, T,
            u_lower=None, u_upper=None,
            u_zero_I=None,
            u_init=None,
            lqr_iter=10,
            grad_method=GradMethods.ANALYTIC,
            delta_u=None,
            verbose=0,
            eps=1e-7,
            back_eps=1e-7,
            n_batch=None,
            linesearch_decay=0.2,
            max_linesearch_iter=10,
            exit_unconverged=True,
            detach_unconverged=True,
            backprop=True,
            slew_rate_penalty=None,
            prev_ctrl=None,
            not_improved_lim=5,
            best_cost_eps=1e-4
    ):

mpc.pytorch